白话 DeepSeek 06|简单而强大的 Transformer
Transformer:抛弃顺序计算的注意力革命
Transformer模型自2017年横空出世,迅速成为自然语言处理(NLP)乃至整个AI领域的基石。它的出现,标志着机器对语言理解方式的一次根本性转变。
在此之前,循环神经网络(RNN)及其变体(如LSTM、GRU)虽然能处理序列数据,但却面临两大顽疾:长期依赖难以有效捕捉(信息在循环中逐层衰减),以及计算必须逐词串行处理(效率低下,无法充分利用GPU的并行能力)。
你有没有想过,如果一个模型能像人类阅读时一样,一眼扫过整个句子,并瞬间权衡每个词与其他词的关系,那将带来怎样的变革?
Transformer的核心正是注意力机制(Attention)—— 一种通过纯矩阵运算并行捕获全局上下文的革命性设计。这种设计不仅极大地提高了效率,更展现了惊人的可扩展性,直接催生了BERT、GPT等一系列划时代的AI巨星。
在本文中,我们将逐步剖析Transformer的设计要点:为什么这样设计?每一步在做什么(包括公式和直观比喻)?如何实现(带维度说明和PyTorch示例代码)?以及优劣与工程提示。适合初学者或希望复习的开发者。
让我们从问题的根源开始:RNN的局限性如何精确地“倒逼”出了Transformer的每一个设计?
输入预处理:词嵌入与位置编码
Transformer的输入不是原始文本,而是经过处理的向量表示。
1. 词嵌入(Word Embedding)
首先,文本中的词汇被转化为高维空间的向量表示,如使用Word2Vec或预训练的嵌入层。这使得模型能捕捉语义相似性(例如,“猫”和“虎”的向量在空间中距离较近)。
2. 位置编码(Positional Encoding, PE)
核心问题:Transformer没有循环结构,它对所有词是并行处理的。如果没有额外的机制,句子“I love AI”和“AI love I”的词向量集合将是完全相同的。你认为这会给理解带来多大的混淆?
解决方案:为了将词汇的位置顺序注入模型,我们添加了位置编码(PE)。
\[\tilde{x}_i = x_i + \text{PE}(i)\]其中,位置编码 $\text{PE}(i)$ 被直接加到词嵌入 $x_i$ 上,形成最终输入向量 $\tilde{x}_i$。一种可解析的位置编码使用正弦和余弦函数,经典的PE使用三角函数::
\[\text{PE}{pos,2k} = \sin\left(\frac{pos}{10000^{2k/d}}\right), \quad \text{PE}{pos,2k+1} = \cos\left(\frac{pos}{10000^{2k/d}}\right)\]$pos$:词在句子中的位置索引(从0开始)。
$k$:维度索引。
$d$:模型维度(通常为512或1024)。
为什么用$sin/cos$?因为它们能编码相对位置,三角恒等式使得任意两个位置的PE可以表示成彼此的线性变换,这意味着模型能够轻松地学习到词语之间的相对距离和位置关系,这对于捕获长距离依赖至关重要。
例如,位置5和位置10的PE可以通过三角恒等式推导出相对距离,便于模型学习长距离依赖。如果说词嵌入赋予了每个词“语义身份”,那么位置编码就像是给它们贴上了一个独特的“时空坐标标签”。模型不仅知道这个词是什么(语义),还知道它在哪里(顺序)。
扩展示例:假设句子“The cat sat on the mat”。词嵌入后,每个词向量为$[0.1, 0.2, …]$,位置0的PE可能为$[sin(0/10000^0), cos(0/10000^0), …]$。添加后,第一个词“The”就有了独特的位置印记。
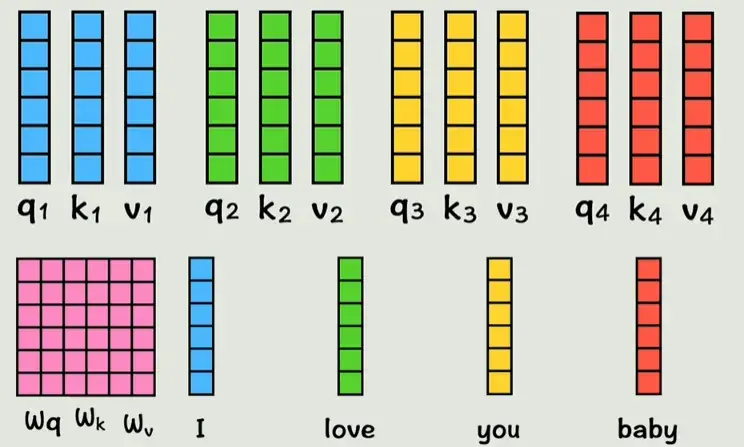
图1:词嵌入通过线性变换(矩阵Wq, Wk, Wv)映射为查询(Q)、键(K)、值(V)。维度不变,通常d=512。这一步为什么重要?因为它允许后续计算词间相似度,而不直接用原始嵌入。
核心机制:缩放点积注意力(Scaled Dot-Product Attention)
现在,每个词都有了位置信息,但它们还是“孤立的”。注意力机制就是让它们“互动”:每个词(查询Q)去“问”其他词(键K)有多相关,然后用相关度权重求和值(V),生成新表示。你有没有好奇,为什么不直接用距离或其他度量,而用点积?
1. QKV 的线性投影
注意力机制不会直接使用原始嵌入向量,而是通过三个独立的线性变换(矩阵 $W^Q, W^K, W^V$)将它们投影到三个不同的空间:
\[Q = XW^Q, \quad K = XW^K, \quad V = XW^V\]其中
Q (Query):查询。代表当前词“我在问什么?”
K (Key):键。代表句子中其他词的“我可以提供什么信息?”
V (Value):值。代表句子中其他词的“我的实际内容是什么?”
为什么要投影? 这一步至关重要,它使得 Q 去寻找 K 的相似度,而不用担心 V 的内容干扰,实现了关注点和内容的分离
2. 缩放点积计算
注意力公式定义了如何用 Q 和 K 计算相似度,并用这个相似度权重对 V 进行加权求和:
\[\text{Attention}(Q,K,V) = \text{softmax}\left(\frac{QK^\top}{\sqrt{d_k}}\right) V\]步骤拆解:
$QK^T$ (相似度计算):计算每个 Query 与所有 Key 的点积。点积值越大,表示两个词之间的相关性越强。
缩放 ($\sqrt{d_k}$):除以 $\sqrt{d_k}$($d_k$ 是 Q 和 K 的维度)。这是为了防止在高维空间中点积结果过大,导致 Softmax 函数进入梯度接近于零的饱和区(即梯度消失)。这一步保证了数值的稳定性和梯度健康。
Softmax (归一化):将相似度转化为概率权重,确保所有权重的总和为1。
加权 V (信息融合):用得到的概率权重对 Value 进行加权求和,生成当前词的全新表示,该表示已融合了整个句子的上下文信息。
比喻深化:想象在一个大型“信息图书馆”里。你(Query)拿着一个借书证去匹配所有书籍的索引卡(Key)。匹配成功的程度(点积)决定了你对这本书的关注度。最终,你将所有被你关注的书籍的内容(Value)按关注度加权汇总,形成了你对整个图书馆知识的新理解。
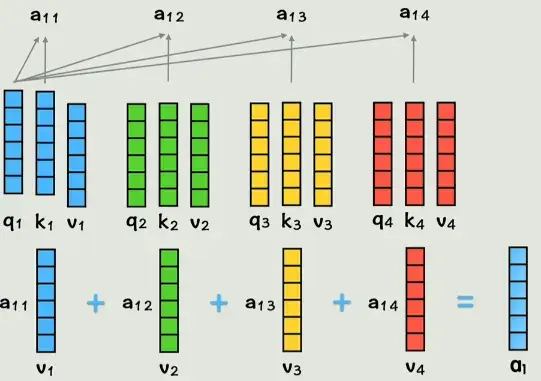
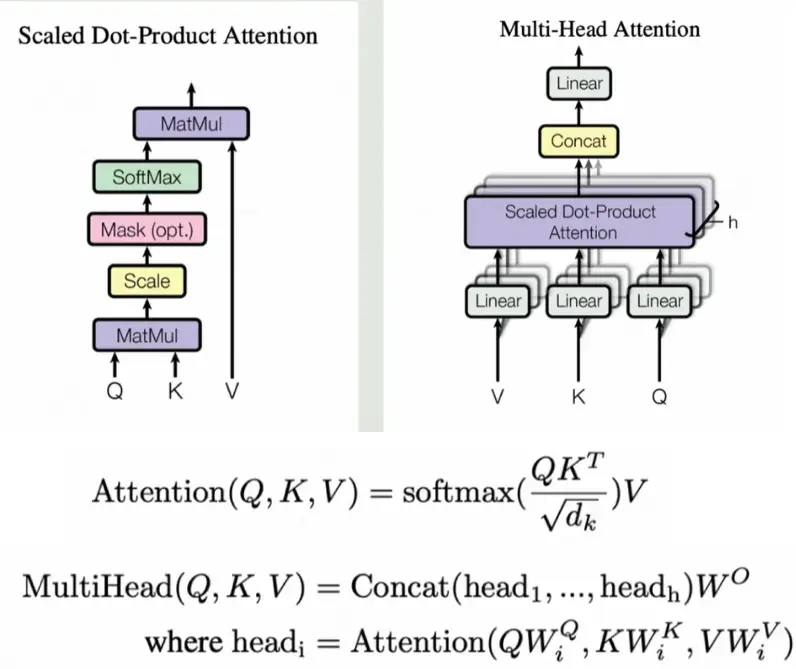
图2:点积相似度计算,权重与V相乘。为什么缩放?高维向量点积易爆炸,缩放保持数值稳定。
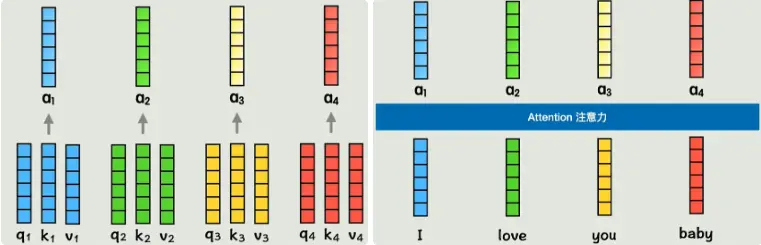
图3:每个输出向量融合全句上下文。补充:可视化注意力热图(heatmap),亮度表示权重,帮助调试模型关注点。
多头注意力(Multi-Head Attention):多角度建模
单一的注意力机制(像只用一个镜头)只能从一个维度建模词间关系。这在处理复杂语义时显得力不从心。你觉得如果用多个“头”,每个专注不同方面(如语法 vs. 语义),会如何提升灵活性?
多头机制(Multi-Head Attention)
多头注意力将模型的总维度 $d_{model}$ 平均分配给 $h$ 个独立的子空间($h$ 为头的数量,通常为8或12)。
\[\text{MultiHead}(Q,K,V) = \text{Concat}(\text{head}_1, \dots, \text{head}_h) W^O\]其中,每个 $head_i$ 独立执行注意力计算:
\[\text{head}_i = \text{Attention}(QW_i^Q, KW_i^K, VW_i^V)\]维度:每个头$d_k = d_{model} / h$。拼接后用$W^O$投影回$d_{model}$。
每个“头”都学习独立的投影矩阵 $W_i^Q,W_i^K,W_i^V$,这意味着它们能够专注于捕捉不同类型的依赖关系。例如,一个头可能关注语法结构(主谓一致),而另一个头可能关注语义关系(同义词、指代消解)。
比喻深化:这就像一个拥有八个摄像头的监控系统,每个摄像头(头)都从不同角度、不同焦距捕捉信息。将所有画面(头输出)拼接在一起,再进行最终处理($W^O$ 投影),所得的综合视图显然比单一视角更加全面、细致。
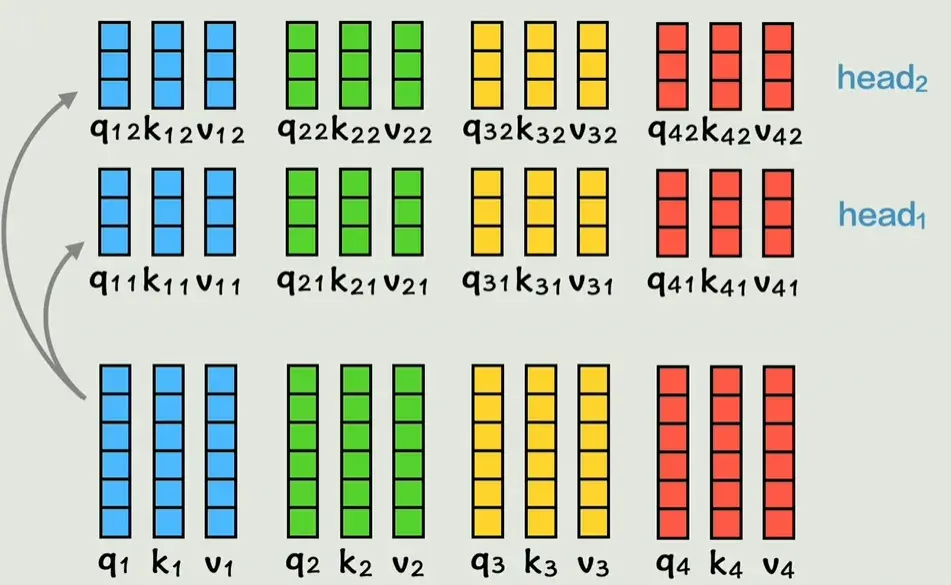
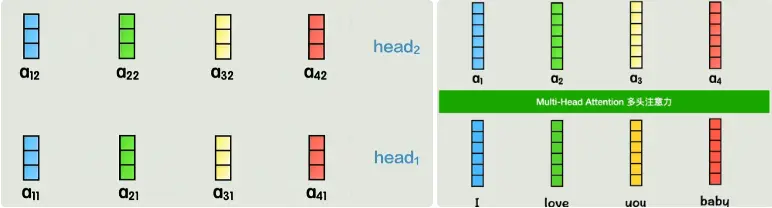
图4:多组QKV,提供多样学习机会。
图5:头输出拼接,再线性变换。补充图片:多头注意力热图,展示不同头关注不同词对。
整体架构:编码器与解码器
Transformer 由 $N$ 层编码器和 $N$ 层解码器堆叠而成(原论文中 $N=6$)。这种分立的设计完美适应了如机器翻译等序列到序列的任务。
1. 编码器层(Encoder)
作用:将输入序列(如英文)转化为一个富含上下文信息的连续表示。
结构:
\[\rightarrow \text{Multi-Head Self-Attention} \rightarrow \text{Add \& Norm} \rightarrow \text{Feed-Forward Network} \rightarrow \text{Add \& Norm} \rightarrow\]自注意力:Q=K=V=输入,关注输入序列内部的关系。
前馈网络(FFN):一个简单的两层全连接网络,通常会将维度扩展到 $4 \times d_{model}$ 再恢复。它独立地作用于序列中的每一个位置,增加模型的非线性拟合能力。
2. 解码器层(Decoder)
作用:接收编码器输出,并自回归地(一个词一个词地)生成目标序列(如法文)。
结构:多了一层“编码器-解码器注意力”。
\[\rightarrow \text{Masked Self-Attention} \rightarrow \text{Add \& Norm} \rightarrow \text{Encoder-Decoder Attention} \rightarrow \text{Add \& Norm} \rightarrow \text{FFN} \rightarrow \text{Add \& Norm} \rightarrow\]Masked Self-Attention (因果遮挡):在训练和生成时,必须确保当前词只能关注它之前的词,不能“偷看”后面的词。一个三角形的因果 Mask 确保了这种自回归特性。
Encoder-Decoder Attention (交叉注意力):
残差连接与 LayerNorm
残差连接(Residual Connection):即 $\text{x} + \text{Sublayer}(\text{x})$。在每个子层(注意力或FFN)之后都添加,它允许梯度直接回流,是训练深层模型时防止梯度消失、稳定训练的关键。
Layer Normalization:在残差连接之后进行,对同一序列的不同特征维度进行归一化,进一步稳定模型的训练。
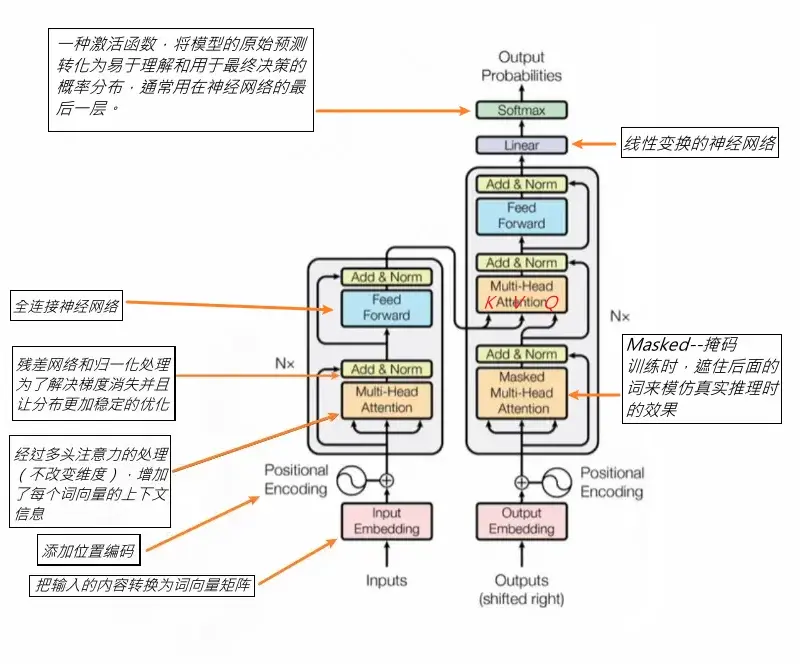
图6:左编码器,右解码器。为什么残差重要?深层模型易梯度消失,残差允许直接流动。
图7:完整公式,包括softmax和缩放。补充:mask可视化,三角形矩阵表示因果遮挡。
优势、局限与变体
卓越的优势
全局并行计算:彻底抛弃串行,计算效率大幅提升,充分利用GPU的并行处理能力。
长距离依赖:通过注意力机制,无论词语相隔多远,关系都可以在一步计算中捕获($O(1)$ 步),完美解决了RNN的痛点。
可解释性:注意力权重热图可以直接显示模型关注的焦点,提供了良好的可调试性。
不可忽视的局限
二次方复杂度:自注意力机制的计算复杂度为 $O(n^2 \cdot d)$,其中 $n$ 是序列长度。对于超长序列(如文本或高分辨率图像),内存和计算开销会呈二次方爆炸。
训练数据需求:Transformer模型参数量巨大,需要海量高质量数据进行训练。
变体与跨模态潜力
Transformer 的强大证明了其架构的通用性。
- BERT:仅使用编码器,侧重于双向上下文理解(适用于分类、抽取)。