白话 DeepSeek 05|从词嵌入到 RNN
全文总结于 Bilibili UP 主飞天闪客的一小时到 Transformer 系列视频!
循环神经网络 RNN(Recurrent Neural Network)
之前的卷积神经网络适合处理图片信息,那文字信息怎么办呢?首先要明白,对于计算机,或者说神经网络来说,文字都是要转换为数字之后再进行处理的。那么我们要面对的第一个问题就是:如何将文字转换为数字
有一种简单粗暴的方法:每一个文字或词组都用一个数字来代表,建一个非常大的映射关系表
但这样有几个显而易见的缺点,第一,只用一个数字表示,不仅要建的表很大,维度也很低(只有一维),第二,数字和数字之间无法表示字与字、词与词之间的联系。为了解决维度低的问题,有人提出了one-hot编码,即准备一个维度非常高的向量,每个字只有向量中一个位置是1,其余全是0。虽然维度低的问题被解决了,但是维度好像又太高了,并且依然没有解决之前的第二个问题。
那有没有能解决以上两种问题的方法呢?有的。这种方法就是词嵌入。
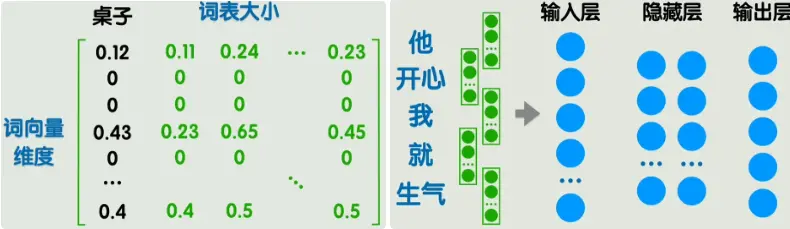
把所有词向量组成一个大矩阵,这个大矩阵就叫做嵌入矩阵,每一列表示一个词向量。矩阵中的值由训练得到,比较经典的方法是word2vec,不展开讲解。虽然这样表示的维度比起one-hot已经大大下降,但是也超过了人能直接理解的二维、三维,我们管这些向量所在的空间叫做潜空间。我们无法理解潜空间中的位置关系,但是也有一些方法能够把潜空间降维至2-3维,方便我们直观看到词与词之间的关系。
这样我们的第一个问题就算是解决了,我们可以用词嵌入的方法将文本转为数据,但这样就可以了吗?举个例子,在右上方的图中,左边的五个词转为5个词向量,每个词向量假设为300维度,那么输入层就要有1500个神经元,当然是可以的,但是有两个新问题:
1.输入层太大了,并且长度不固定;
2.无法体现词语的先后顺序,参考之前无法体现图片像素的位置关系。在之前的图像处理中,我们可以通过卷积的方式来解决这一问题,那现在呢?
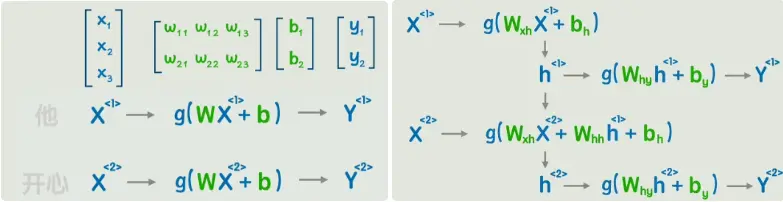
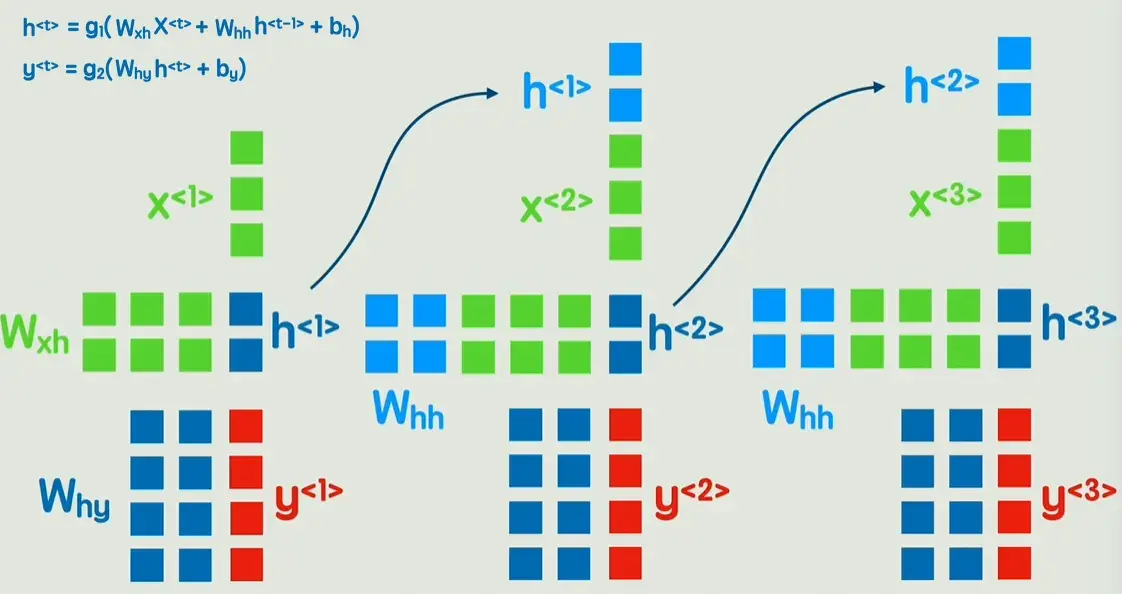
回到经典的神经网络,但是不是一次输入一句话,而是输入一个词。当然这里的X、W都是矩阵,之后不再展开。
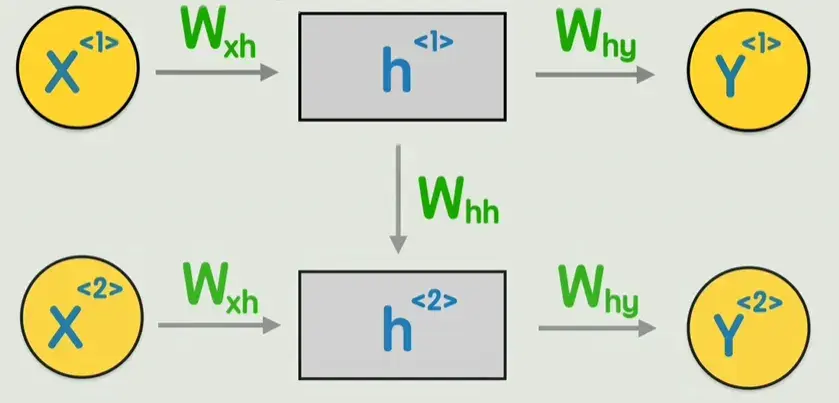
可以发现在第二个词的计算过程中,完全没有让第一个词的任何信息参与进来,怎么办呢?可以像右图这样,先输出一个隐藏状态,然后再经过一次非线性变换,得到输出Y。这就是循环神经网络RNN。
这个RNN模型就具备了理解词与词之间先后顺序的能力,可以判断一句话中各个单词的褒贬词性,还能给出一句话,不断生成下一个字,以及完成翻译等自然语言处理工作。
那么RNN是否就完美了呢?当然不,RNN依旧存在两个问题:
1、信息会随着时间步的增多而逐渐丢失,无法捕捉长期依赖,而有的语句的关键信息恰好在很远的地方
2、RNN必须顺序处理,每个时间步必须依赖上一个时间步的隐藏状态的计算结果
虽然有一些方法在改进以上两点问题,但是还不够好,那么是否有一个可以彻底抛弃按顺序计算的新方案呢?
有的兄弟,有的,那就是Transformer!
从词到句的记忆:循环神经网络 RNN 深度讲解
一、从图片到文字:神经网络的新挑战
在上一篇中,我们谈到了卷积神经网络(CNN)如何高效处理图像信息 —— 它能捕捉空间结构(像素的局部关系)。
但如果任务目标换成“理解文字”呢?
图像是二维的,文字却是一维的序列 —— 时间顺序(或语序)才是关键。
于是问题出现了:
对于计算机,或者说神经网络来说,文字都是要转换为数字之后再进行处理的。在进入神经网络之前,我们得先让“文字”变成机器能理解的“数字”。
二、文字数字化:从简单编码到语义空间
1️⃣ 方法一:数字映射(Index Mapping)
有一种简单粗暴的方法:每一个文字或词组都用一个数字来代表,建一个非常大的映射关系表,比如:
然后“我爱北京天安门”就可以表示为 [1, 2, 3, 4]。
这种方法虽然简单,但有几个显而易见的缺点:
数字之间没有语义关系;
每个词只对应一个数字,不仅要建的表很大,而且信息维度太低(只有一维);
数字和数字之间无法表示字与字、词与词之间的联系,无法表达“我”和“我们”之间的相似性。
2️⃣ 方法二:One-Hot 编码(独热向量)
为每个词创建一个长度为词表大小的向量(维度非常高)
只有该词对应的位置为 1,其余为 0。
例如,假设词表大小为 5:
优点:能避免整数编码的排序误导。
缺点:
向量极度稀疏(高维、低信息);
不同词语仍然完全独立,并没有解决词与词之间的相关联关系(语义信息)。
3️⃣ 方法三:词嵌入(Word Embedding)——让词语“活”起来
词嵌入的核心思想是:
用一个低维、稠密向量来表示词语,并让向量之间的几何关系体现语义关系。
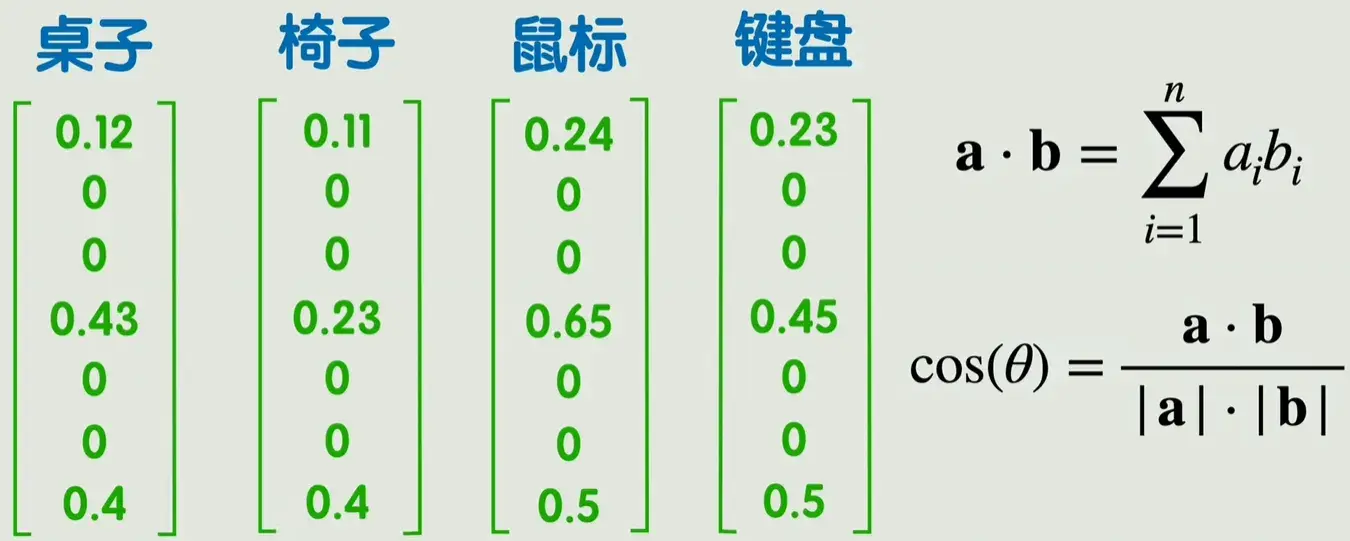
可以用两个向量的点积或余弦相似度来表示向量之间的相关性,进而表示词语之间的相关性。
这样就将自然语言之间的联系转为可以用数学公式计算的方式。同时,一些数学上的计算结果可能反映出一些很微妙的关系,例如一个训练好的词嵌入矩阵,很可能使得桌子-椅子 = 鼠标 - 键盘。
✳️ 例子
“桌子”“椅子”可能在语义空间中非常接近,
而 “桌子” - “椅子” ≈ “鼠标” - “键盘”,
说明模型确实学会了语义对应。
✳️ 数学上
每个词是一个向量 $v_i \in \mathbb{R}^d$,
通过余弦相似度表示语义相似性:
\[\text{similarity}(v_i, v_j) = \frac{v_i \cdot v_j}{||v_i|| \cdot ||v_j||}\]所有词向量拼起来构成一个大矩阵 —— 嵌入矩阵(Embedding Matrix)。每一列表示一个词向量。矩阵中的值由训练得到,
它由训练学习而来,常见的训练算法有 Word2Vec、GloVe 等。
4️⃣ 潜空间(Latent Space)与可视化
词嵌入的维度通常为 100~300 维,超过了人能直接理解的二维、三维,人类无法直接理解。
但通过降维(如 PCA、t-SNE),方法能够把潜空间降维至2-3维,方便我们直观看到词与词之间的关系。可以在二维平面上看到“语义结构”:
这就是语言的潜空间:
高维中隐藏着词语之间的关系,而模型通过训练自动“发掘”它。
三、从词到句:序列的挑战
现在我们能把词转成向量了。我们可以用词嵌入的方法将文本转为数据,但这样就可以了吗?
比如一句话含有 5 个词,每个词 300 维 → 整体输入就是 1500 维。
新的问题来了:
1️⃣ 长度不固定:每句话的词数不同。
2️⃣ 顺序无法体现:向量相加或拼接后,神经网络并不知道哪个词在前哪个词在后。
在图像里,我们用卷积捕捉位置关系;
在文本里,我们需要一种能理解“前后依赖”的机制。
四、让网络“记忆”:RNN 的诞生
回到经典的神经网络,但是不是一次输入一句话,而是输入一个词。当然这里的X、W都是矩阵,之后不再展开。
它一次性处理所有输入,没有上下文依赖。
完全没有让第一个词的任何信息参与进来,怎么办呢?可以像右图这样,先输出一个隐藏状态,然后再经过一次非线性变换,得到输出Y。
输入“今天”“天气”“很好”三个词时,
“很好”这个输出不会受到“今天天气”的影响。
这时,RNN(循环神经网络)登场了。
五、RNN:让神经网络有“记忆”的结构
RNN 的核心思路是:
在处理当前输入 $x_t$ 的同时,
还要考虑上一时刻的隐藏状态 $h_{t-1}$。
计算过程如下:
\[h_t = f(W_{xh}x_t + W_{hh}h_{t-1} + b_h)\] \[y_t = g(W_{hy}h_t + b_y)\]