白话 DeepSeek 04|从矩阵到 CNN
全文总结于 Bilibili UP 主飞天闪客的一小时到 Transformer 系列视频!
矩阵表示、卷积与 CNN:从“密集连接”到“局部共享”的直观演绎
本篇目标:
一、回到矩阵表示:把复杂式子变得简洁且可并行
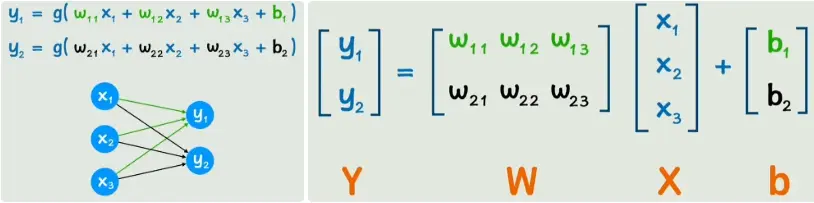
当网络刚开始只有少量节点时,我们可以直接用元素级公式写出每个神经元的输出。但随着层数和每层节点数增长,逐个写式子既繁琐又不利于数学推导与实现。用矩阵把这些运算“打包”起来既直观又高效。
常见的一层前向传播(全连接)可以写成:
\[a^{[l]} = \sigma\big(W^{[l]} a^{[l-1]} + b^{[l]}\big)\]其中:
$(a^{[l-1]})$ 表示上一层(或输入层)的激活向量;
$(W^{[l]})$是当前层的权重矩阵(形状:$n_l, n_{l-1}$);
$(b^{[l]})$ 是偏置向量;
$(\sigma(\cdot))$ 是逐元素激活函数($ReLU、sigmoid$ 等)。
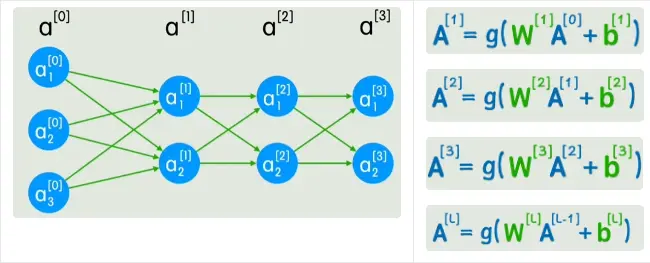
把层级用下标/上标表示($a^{[0]}$ 为输入,$a^{[1]}$、$a^{[2]}$ ……为中间层),就能用统一的通式描述任意深度网络的前向传播。这种矩阵表达的好处有两点:
抽象清晰:便于推导反向传播(链式法则在矩阵形式下更整洁)。
高效并行:矩阵乘法可以很好利用 BLAS、cuBLAS 等库与 GPU 并行加速,训练与推理更快。
二、全连接层在图像任务上的天然问题
回到图像问题:很多入门教材会先把图像“扁平化”成向量,然后通过全连接层处理——这在概念上是可行的,但实际存在三大问题:
1)参数数目爆炸
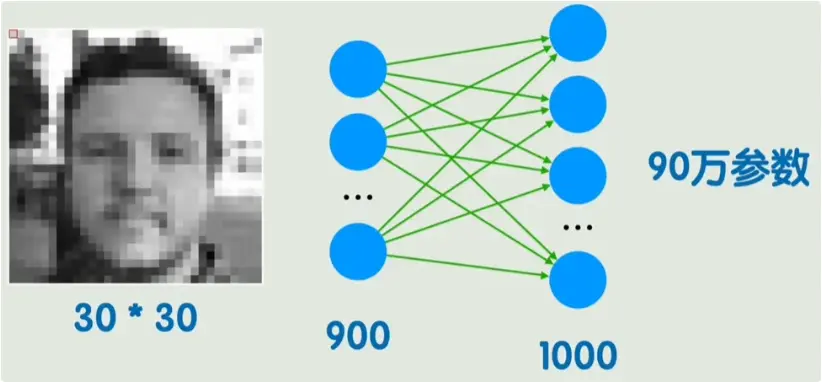
例如:灰度图 30×30 → 900 个输入像素;若接一个 1000 单元的隐藏层,参数量:
\[900 \times 1000 = 900{,}000\](再加上偏置项约 1000),已接近百万级别。对于彩色大图(如 $224×224×3$ )则远超可承受范围。
2)丢失空间结构
图像像素有明显的二维邻接关系(局部相关性)。把它平铺后,像素位置的信息被破坏——模型无法直接利用“邻域”的先验(比如边缘、角点等是局部特征)。
3)对平移/局部扰动敏感
若图中物体轻微平移或有局部噪声,平铺索引变化会导致几乎所有全连接权重输入都发生变化,模型难以稳定识别同一局部模式。
用户提供的图示正好展示了这些问题:节点与上一层所有节点相连(全连接),产生大量权重并忽略像素之间的位置信息。
三、卷积运算:把“局部 + 共享”搬到网络里
为了解决上述问题,我们把注意力转向 卷积运算(convolution)。直观做法是:在输入图像上滑动一个小窗(例如 3×3),把窗口内像素与一个同大小矩阵做对应位置相乘并求和,结果放到输出特征图的对应位置。这个 3×3 的小矩阵就是 卷积核(filter / kernel) 或称权重模板。
简图如下(示意卷积核在图片上滑动并产生输出):
卷积的三大核心思想(再次总结)
局部感受野(Local receptive field):每个输出只由输入的局部子区域决定(例如 3×3)。
权重共享(Weight sharing):同一个卷积核在整张图上重复使用,检测相同的模式(如“水平边缘”)在不同位置的存在。
平移等变/不变:卷积输出会随着输入平移而平移,后续的池化或全局汇聚操作使得整体识别对平移更不敏感(近似不变)。
四、从数学上看:矩阵乘法 → 卷积运算的替代
经典全连接层是矩阵乘法:(W a)。卷积则是局部乘加的线性算子。在实现层面,卷积通常可以被转化为矩阵乘法(例如 im2col/unfold 将滑动窗口展开成列,然后做一次巨大的矩阵乘法),这使得卷积同样能高效地利用 GPU(矩阵乘法的高速库)。因此,从“并行化”角度来看,卷积并不会在速度上落后,反而在参数效率和特征可重用性上占优势。
五、参数量比较(用数字说话)
继续用之前的例子(单通道 30×30 图像):
全连接: 输入 900,输出 1000 → 参数约 900 × 1000 = 900000。
卷积(例): 卷积核 3×3,使用 16 个滤波器(输出通道 16)→ 参数数为:
同样的表征能力(检测局部边缘/角点/纹理),卷积用的参数只是全连接的一小部分,因此学习更高效、抗过拟合能力更强。
六、结构上:卷积 + 池化 + 全连接 = 卷积神经网络(CNN)
把卷积层堆叠起来可以逐级抽象:
低层学到边缘、颜色斑块;
中层学到纹理、组合形状;
高层学到语义更强的部分(如眼睛、轮廓)。
中间常常搭配 池化(Pooling) 操作来下采样(降低特征图的空间分辨率)并保留主要特征,从而减少计算量与参数,同时增加平移不变性。常见池化有:
Max Pooling:取局部区间最大值(常用于保留最显著响应)
Average Pooling:取局部区间平均值(平滑)
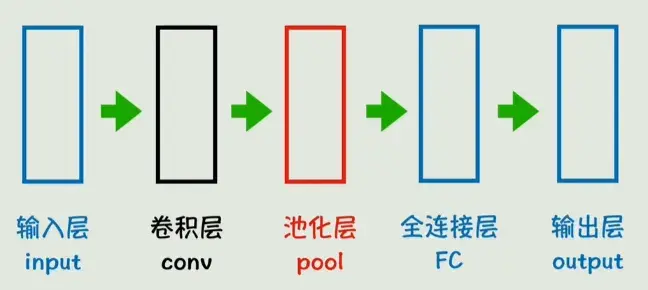
最终在网络后端仍可能接入若干 全连接层 做最终判别(例如类别预测)。整体结构示意:
七、简单代码示例(PyTorch)——对比参数与输出形状
下面是一个简短可运行的 PyTorch 代码片段(注释充分),演示把图像扁平化接全连接 vs 使用卷积层,并统计参数数目与输出形状(继续用单通道 30×30 为例):
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import torch
import torch.nn as nn
# 假设输入:batch=8, channels=1, H=W=30
x = torch.randn(8, 1, 30, 30)
# 全连接方案:flatten -> Linear(900 -> 1000)
class FCModel(nn.Module):
def __init__(self):
super().__init__()
self.fc = nn.Linear(30*30*1, 1000)
self.act = nn.ReLU()
def forward(self, x):
x_flat = x.view(x.size(0), -1) # flatten: [B, 900]
out = self.fc(x_flat) # linear: [B, 1000]
return self.act(out)
fc = FCModel()
print("FC params:", sum(p.numel() for p in fc.parameters()))
print("FC out shape:", fc(x).shape) # -> [8, 1000]
# 卷积方案:Conv2d(1 -> 16, kernel=3, padding=1) -> ReLU
class ConvModel(nn.Module):
def __init__(self):
super().__init__()
self.conv = nn.Conv2d(1, 16, kernel_size=3, padding=1)
self.act = nn.ReLU()
def forward(self, x):
out = self.conv(x) # output: [B, 16, 30, 30]
return self.act(out)
conv = ConvModel()
print("Conv params:", sum(p.numel() for p in conv.parameters()))
print("Conv out shape:", conv(x).shape) # -> [8, 16, 30, 30]
运行这段代码可以直观看到:全连接参数数目远大于卷积,而卷积输出保留了空间维度(可进一步做池化 / 下采样)。
八、卷积核的“可学习性”与传统图像处理的差异
在传统图像处理里(如用 Sobel、Laplacian 等算子),卷积核是手工设定的,目标是求边缘、模糊或锐化。这些核是固定的,不参与学习。
在 CNN 中,卷积核是可学习参数:通过梯度下降等优化方法自动学习出“对当前任务最有用”的滤波器(例如检测某类边缘、纹理或形状)。这使得 CNN 在复杂视觉任务上具有极强的表达与适应能力。
九、局限性与扩展(何时不该只用 CNN?)
虽然 CNN 在静态图像识别中非常成功,但也存在一些局限或需要注意的场景:
时序/序列数据(文本、音频、视频)
全局上下文捕获能力
旋转/尺度等不变性
十、结语与后续主题建议
小结:
用矩阵表示把神经网络的前向传播抽象为 (a^{[l]}=\sigma(W^{[l]}a^{[l-1]}+b^{[l]})),既清晰又利于 GPU 加速;
全连接层在图像任务中参数巨大且丢失空间结构;
卷积通过“局部感受野 + 权重共享 + 池化”在参数效率和对局部模式的捕捉上有显著优势,从而催生了 CNN 在视觉领域的主导地位;
CNN 并非万金油,其在序列任务或需要全局建模的场景下有替代方案(RNN、Transformer、1D/3D conv 等)。
后续建议(可作为下一期播客/文章主题):
把“卷积如何在 GPU 上被优化(im2col、卷积算法)”讲清楚;
深入讲解“卷积核可视化/解释”与“不同层学到的特征”;
讲解池化类型、步幅(stride)、填充(padding)对输出尺寸与信息保留的影响;
比较 CNN、RNN、Transformer 在不同任务(图像、文本、音频、视频)上的优劣并给出工程实践建议。